13, 20, 27 травня
Тема 8.Основні напрямки сучасної логіки
1)Індукційні логіки. (13 травня)
Історія розвитку логіки
3)Модальні, позитивні, багатозначні логіки. (27 травня)
Модальні висловлювання - це висловлювання, в які входять модальні поняття, або модальності (від лат. Modus - міра, образ, спосіб).
Прикладами модальних понять можуть служити поняття: «можливо», «необхідно», «випадково», «переконаний», «знає», «вважає», «обов'язково», «дозволено», «заборонено», «добре», «байдуже» , «погано», краще »,« гірше »і т. д.
8, 15, 22, 29 квітня, 6 травня
Тема 7. Логічний практикум
10, 18, 25 березня
Тема 6. Логічні основи теорії аргументації
1) Поняття доказу і його структури. Види аргументів. Пряме і непряме підтвердження. (10 березня)
2) Поняття спростування та його види. Правила доказового міркування. Логічні помилки в доказах.(18 березня)
3) Поняття софізму і логічних парадоксів. Мистецтво ведення дискусії. (25 березня)
Тема 8.Основні напрямки сучасної логіки
1)Індукційні логіки. (13 травня)
Історія розвитку логіки
Індукція та її роль в пізнанні.
Індукція: метод наукового пізнання, який полягає в дослідженні руху знань від одиничного до часткового або й загального; вид опосередкованого умовиводу, в якому з одиничних суджень-засновків виводять часткове або й загальне судження-висновок
Види індуктивних умовиводів
Розрізняють повну індукцію, засновки якої вичерпують увесь клас предметів, що підлягає індуктивному узагальненню, і неповну індукцію, засновки якої не вичерпують усього класу предметів, що підлягають такому узагальненню.
Повна індукція
Повна індукція - індуктивний умовивід, у якому на підставі знання про належність певної ознаки кожному предметові класу робиться висновок про належність цієї ознаки всім предметам цього класу.
Оскільки повна індукція передбачає виявлення певної ознаки в кожному предметі відповідної множини, то висновок її (повної індукції) має достовірний характер. Схема міркування за повною індукцією така:
S. є Р S2eP S3eP
S'e'p'
n
Відомо, що Sr S2, S "..., Sn вичерпують усю множину предметів класу S.
Отже, всі S є Р.
Наприклад:
- Меркурій обертається навколо Сонця.
- Венера обертається навколо Сонця.
- Земля обертається навколо Сонця.
- Марс обертається навколо Сонця.
- Юпітер обертається навколо Сонця.
- Сатурн обертається навколо Сонця.
- Уран обертається навколо Сонця.
- Нептун обертається навколо Сонця.
- Плутон обертається навколо Сонця.
Відомо, що Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун і Плутон вичерпують усю множину планет Сонячної системи.
Отже, всі планети Сонячної системи обертаються навколо Сонця.
Повна індукція відрізняється від дедукції вже тим, що вона не дає знання про інші предмети, крім тих, які мисляться в одиничних судженнях-засновках. Разом з тим вона подібна до дедукції принаймні достовірністю своїх висновків. Абсолютизуючи подібність повної індукції та дедукції, деякі логіки відмовляють їй у статусі індукції. Інколи вважають, ніби повна індукція неспроможна дати нові знання. Проте вона відповідає загальному визначенню індуктивного умовиводу.
Стосовно новизни висновків за повною індукцією слід розрізняти знання про належність тієї чи іншої ознаки кожному предметові відповідного класу і знання про належність цієї ж ознаки всім предметам цього класу. Адже загальний висновок повної індукції хоч і характеризує ті самі предмети, але дещо з іншого боку - з боку їх родової належності.
Гідно оцінюючи роль повної індукції, разом з тим треба визнати, що в реальному людському пізнанні вона займає незначне місце, оскільки до неї вдаються тільки при пізнанні скінченних і осяжних класів предметів (йдеться насамперед про ті класи предметів, які відображаються в реєструючих поняттях).
В особливий різновид індуктивних умовиводів виділяють так звану математичну індукцію, яка ґрунтується на специфіці будови і властивостях натурального ряду чисел. У натуральному ряді чисел кожне число більше від попереднього на одиницю. Хід міркування за формою математичної індукції такий: якщо якась ознака характерна для числа 1 і якщо ця ж ознака, будучи характерною для довільного числа натурального ряду п, належить і наступному числу п+1, то ця ознака характерна для всіх чисел натурального ряду.
Схема математичної індукції:
- Якщо Р (1);
- Якщо Р (п), то Р (п+1);
- Отже, V х Р (х).
Неповна індукція
Неповна індукція - індуктивний умовивід, у якому висновок про весь клас предметів робиться на підставі знання тільки деяких предметів цього класу.
Наведемо два приклади таких умовиводів:
1. Залізо - електропровідне.
- Мідь - електропровідна.
- Свинець - електропровідний.
- Срібло - електропровідне.
- Золото - електропровідне.
- Залізо, мідь, свинець, срібло, золото - метали.
- Отже, всі метали - електропровідні.
2. Залізо тоне у воді.
- Мідь тоне у воді.
- Свинець тоне у воді.
- Срібло тоне у воді.
- Золото тоне у воді.
- Залізо, мідь, свинець, срібло, золото - метали.
- Отже, всі метали тонуть у воді.
Обидва умовиводи побудовані за схемою неповної індукції й ґрунтуються на істинних засновках. Проте висновок першого умовиводу є істинним, а другого - хибним. Оскільки засновки в другому умовиводі є істинними, то причиною хибності його висновку може бути лише недосконалість міркування, побудованого за схемою неповної індукції.
Річ у тім, що в підґрунті індуктивного методу немає логічного закону, який би гарантував одержання істинного висновку з істинних засновків. Тому неповна індукція дає ймовірний висновок. Пам'ятаючи про це, висновок із неповною індукцією треба розпочинати словами "мабуть", "напевно" тощо.
Імовірний умовивід - умовивід, в якому з істинних засновків певної структури одержують висновок, що може бути як істинним, так і хибним.
Крім неповної індукції, до ймовірних умовиводів належить також аналогія. Для визначення того, яким є висновок імовірного умовиводу - істинним чи хибним, - доводиться вдаватися до додаткової інформації. Для ймовірних умовиводів, на відміну від достовірних, не можна сформулювати таких правил, при дотриманні яких висновок неодмінно буде істинним, якщо вони застосовуватимуться до будь-яких істинних конкретних за змістом засновків певної структури.
Імовірність - величина, яка характеризує "ступінь можливості" якоїсь події, що може як відбутися, так і не відбутися.
Вивчаючи ймовірні умовиводи, увагу акцентують на ймовірнісній оцінці ступеня обґрунтованості (підтверджуваності) суджень-висновків. У логічній науці розробляють спеціальні методи оцінки ймовірності висновків, одержаних за схемою неповної індукції.
Неповну індукцію поділяють на популярну (народну) і наукову.
Популярна індукція - неповна індукція через простий перелік за відсутності суперечного випадку.
У цій індукції узагальнення ґрунтується на фактах повторюваності однієї й тієї самої ознаки в кількох чи й багатьох предметах певного класу і відсутності суперечного цій повторюваності випадку. Так, численні факти ефективності ліків, виготовлених деякими майстрами народної медицини, дають можливість зробити загальний висновок про її ефективний вплив на організм людей.
Це міркування є прикладом популярної індукції за умови, що представник народної медицини не знає причинного зв'язку, який діє між його ліками і людським організмом, а знає лише те, що в усіх випадках застосування даних ліків не було жодного негативного наслідку. Простий перелік - це лише один перелік без будь-якої іншої додаткової інформації, крім, звичайно ж, знання про відсутність суперечного випадку.
Був час, коли популярну індукцію переважно критикували, проте вона є тією "матір'ю", яка народжує то недолугих дітей (різного роду забобони), то геніїв (народну мудрість). Внутрішні, необхідні зв'язки речей, закономірності являються буденній свідомості у формі повторюваності. Ця повторюваність (разом з іншими чинниками) відіграла не останню роль у виникненні людського мислення. Проте не кожна повторюваність має своїм підґрунтям необхідні зв'язки між речами. Ототожнювання випадкової повторюваності з необхідною, часової та просторової послідовності подій - з причинною їх пов'язаністю призводить до логічних та фактичних помилок.
Типовими помилками, які трапляються при некритичному ставленні до популярної індукції, є "поспішне узагальнення", "після цього - внаслідок цього" тощо. Виявами таких помилок є різноманітні забобони та марновірства. До речі, і перлини народної мудрості, зокрема народної медицини, потребують обґрунтування, виявлення відповідних причинних зв'язків, у результаті чого вони набудуть статусу наукових істин.
Наукова індукція - неповна індукція, в якій на підставі пізнання необхідних ознак деяких предметів певного класу робиться загальний висновок про всі предмети цього класу.
За схемою міркування (від знання окремих предметів певного класу до знання всього класу) наукова індукція не відрізняється від популярної. Відмінність її полягає в характері та природі засновків і способі їх підбору.
Якщо в популярній індукції засновки для узагальнення беруть переважно випадково, то в науковій їх підбирають свідомо, з урахуванням того, наскільки істотними є зв'язки, які в них відображаються. При цьому великого значення надають причинно-наслідковим зв'язкам речей. Автори, що вдаються до наукової індукції, не задовольняються відомими фактами. Вони одержують факти, використовуючи такі методи, як порівняння, вимірювання, спостереження, експеримент.
Сила наукової індукції полягає в тому, що кожний її крок пов'язаний з фактами, досвідом, вона часто піддається перевірці. А слабкість - у тім, що всезагальні висновки не піддаються перевірці емпіричними засобами, тобто з допомогою верифікації.
Оцінюючи пізнавальні можливості наукової індукції, треба пам'ятати і про історичну обмеженість людського досвіду.
Методи встановлення причинних зв'язків
Добираючи засновки для наукової індукції, часто вдаються до методів виявлення причинних зв'язків між явищами.
Причинні зв'язки між предметами і явищами не існують у чистому вигляді. Вони завжди супроводжуються безліччю інших зв'язків, зокрема тими обставинами, які забезпечують їх реалізацію. Все це ускладнює процес встановлення причинних зв'язків між явищами.
Існує п'ять методів виявлення причинних зв'язків між явищами:
- метод єдиної подібності;
- метод єдиної відмінності;
- поєднаний метод подібності та відмінності;
- метод супутніх змін;
- метод залишків.
Усі перелічені методи ґрунтуються на таких рисах причинного зв'язку:
- кожне явище має причину, тому пошуки її виправдані;
- причина завжди передує наслідку, тобто тому явищу, причину якого ми прагнемо встановити;
- після причини неодмінно настає явище-наслідок;
- за відсутності причини наслідок не настає;
- зміни в причині призводять до відповідних змін у наслідку.
Метод єдиної подібності. Сутність цього методу полягає у виявленні серед численних умов, що передують досліджуваному явищу, такої умови, яка постійно йому передує.
Метод єдиної подібності: якщо певна обставина постійно передує досліджуваному явищу при несталості всіх інших обставин, то, ймовірно, саме вона є причиною явища.
Наприклад: в одній із їдалень міста сталися три випадки отруєння людей, які там обідали. При цьому стало відомо, що відвідувач їдальні А. споживав першу, другу і третю страви; відвідувач Б. - другу і третю; а відвідувач В. - лише другу:
- За умов 1, 2, 3 мало місце отруєння.
- За умов 2, 3 мало місце отруєння.
- За умови 2 мало місце отруєння.
Отже, найбільш імовірно, що саме умова 2 (друга страва) була причиною отруєння.
Схема методу:
- АВС-*а.
- ABDa.
- 3-. ACDa.
Отже, причиною явища а є обставина А.
Метод єдиної відмінності. Метод єдиної відмінності: якщо певна обставина наявна тоді, коли настає досліджуване явище, і відсутня тоді, коли це явище не настає (а все інше залишається незмінним), то ця обставина і є ймовірною причиною цього явища.
Наприклад: двоє людей пообідали в одній із їдалень міста. Причому, та людина, що споживала першу, другу і третю страви, отруїлася, а друга, яка споживала лише першу і третю страви, залишилася здоровою:
- За умов 1, 2, 3 мало місце отруєння.
- За умов 1, 3 отруєння не було.
Отже, найімовірніше, що причиною отруєння була умова 2 (друга страва).
Схема методу:
- АВСа
- ВС-*-
Отже, обставина А є причиною явища а.
Поєднаний метод подібності та відмінності. Поєднаний метод подібності та відмінності: якщо два чи більше випадків, коли виникає досліджуване явище, подібні лише однією обставиною, яка передувала виникненню цього явища, а два чи більше випадків, коли це явище не виникає, відрізняються тільки тим, що ця обставина була відсутньою, то ця обставина, ймовірно, і є причиною досліджуваного явища.
Наприклад: в одній з їдалень міста обідали четверо людей. При цьому троє з них отруїлися, а четвертий, який сидів з ними за одним столом, залишився здоровим. Стало відомо, що відвідувач цієї їдальні А. споживав першу, другу і третю страви; відвідувач Б. - другу і третю; відвідувач В. - лише другу; відвідувач Г. - першу і третю.
З'ясувавши, що перші три відвідувачі зазнали отруєння, а четвертий залишився здоровим, можна зробити висновок, що саме друга страва була причиною отруєння. Це пояснюється, по-перше, тим, що єдиною подібною обставиною для всіх, хто зазнав отруєння, було споживання ними другої страви, а по-друге - єдиною обставиною, якою відрізнялася людина, яка залишилася здоровою, від усіх інших, було те, що вона не споживала другої страви.
Схема методу:
- АВС->а
- АВ-а
- А-а
- ВС-*-
Отже, обставина А є причиною явища а.
Метод супутніх змін. Виявити причину досліджуваного явища можна не лише за наявністю чи відсутністю її серед інших обставин, які передували виникненню цього явища, а й за тими змінами, які відбуваються в наслідку, під впливом змін у причині.
Метод супутніх змін: якщо зі зміною однієї з обставин, що передують виникненню досліджуваного явища, змінюється і саме явище, то, ймовірно, що саме ця обставина є причиною виникнення цього явища.
Наприклад: ґрунт, на якому були посаджені помідори, підживили невеликими дозами калію, азоту і фосфору. Рослини нормально розвивалися. Господар вирішив різко збільшити кількість азотних добрив, не вносячи в ґрунт ні калійних, ні фосфорних. Результат не примусив на себе довго чекати — помідори стали швидко збільшувати вегетативну масу. Звідси було зроблено висновок, що причиною швидкого збільшення вегетативної маси помідорів є азотні добрива.
Схема методу:
- ABCD-abcd.
- AfiCDaficd.
- AfiCD-aficd.
Отже, обставина А є причиною явища а.
Метод залишків. Цей метод передбачає наявність комплексу обставин (причин) і комплексу їх дій (наслідків). Якщо існують обставини ABC, спостерігаються їх дії abc, і відомо, що обставина В є причиною Ь, обставина С - причиною с, а причина а невідома, то в даному разі, виключивши обставини В і С, які породжують явища b і с, робиться припущення, що А є причиною а.
Метод залишків: якщо дві чи більше сукупних причин породжують стільки ж сукупних явищ (наслідків) і відомо, що частина цих причин породжує відповідну частину явищ, то залишкова причина, ймовірно, породжує останню частину явищ.
Схема методу:
- ABC-abc ВСЬс.
Отже, А є причиною а.
Роль індукції в процесі пізнання
Важко перебільшити місце і значення індукції в процесі пізнання. Особливо велику роль вона відіграла на зорі історії, коли люди користувалися лише обмеженою кількістю загальних понять. Та і в наш час без індукції не обійтися.
Щоб збагнути справжнє значення індукції в житті людей, треба враховувати не лише її наукову цінність, а й роль у повсякденному житті. Навіть у формуванні світогляду (особливо світобачення, ставлення до дійсності та переживання буття) індукція відіграє істотну роль. Правда, щоб визнати це, треба належно оцінити силу впливу особистісного життєвого досвіду на процес становлення особистості.
Разом з тим не можна не брати до уваги ймовірний характер індуктивного узагальнення. Тому необхідно постійно працювати над підвищенням імовірності висновків, одержаних за схемою неповної індукції. З цією метою треба використовувати якомога більше засновків (збільшувати число випадків, які узагальнюються), урізноманітнювати досліджувані випадки, враховувати характер зв'язку між досліджуваними явищами та їх ознаками.
З метою підвищення ймовірності висновків неповної індукції вдаються до різноманітних методів встановлення причинних зв'язків між явищами.
Виконай завдання
Завдання 1. (13,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю
2)Конструктивні логіки. (20 травня)
Інтуїтивна логіка (інколи конструктивна логіка) — система символічної логіки, яка відрізняється від класичної логіки, замінюючи традиційне поняття істини поняттям конструктивно доказової істини. Наприклад, у класичній логіці, пропозиціональні формули (предикати) завжди приймають значення істинності з множини двох тривіальних елементів тверджень («істина» і «хиба» відповідно) незалежно від того, чи є у нас прямий доказ для будь-якого випадку. Навпаки, пропозиціональним формулам (предикатам) в інтуїтивній логіці взагалі не надається ніякого певного значення істинності: натомість вони вважаються «істинними» лише тоді, коли у нас є прямий доказ. (Замість «формула істинна на основі прямого доказу» можна також сказати, що формула уможливлена доказом у сенсі Каррі — Говарда). Тому операції в інтуїтивній логіці зберігають юстифікацію (виправдання), щодо доказу та доказової операції, а не оцінки істини.
Завдання 2.(20,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю
Завдання 2.(20,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю
Модальні висловлювання - це висловлювання, в які входять модальні поняття, або модальності (від лат. Modus - міра, образ, спосіб).
Прикладами модальних понять можуть служити поняття: «можливо», «необхідно», «випадково», «переконаний», «знає», «вважає», «обов'язково», «дозволено», «заборонено», «добре», «байдуже» , «погано», краще »,« гірше »і т. д.
Прочитай Модальні висловлювання
Позити́вна ло́гіка — частина числення висловлювань, у певному розумінні незалежна від наявності заперечення. Позитивну логіку побудували Давид Гільберт і П. Бернайс (в 1934), відкинувши від аксіоматики Гільберта єдину аксіому, що містить заперечення.
Позитивну логіку можна побудувати, використовуючи лише одну логічну зв'язку — імплікацію (позитивне імплікативне пропозиційне числення).
Переваги
Перевага позитивної логіки в тому, що в ній у зручному вигляді представлено зв'язок між класичним та інтуїціоністським численням висловлювань. В. І. Гливенко (1929) зробив висновок, що, додаючи до позитивної логіки певні аксіоми з символом заперечення, можна одержати інтуїціоністське пропозиційне числення, а додаючи до останнього виключеного третього закон — повне (класичне) пропозиційне числення.
Опрацюй Багатозначна логіка
Прочитай ДОДАТОК ЛОГІЧНИЙ ПРАКТИКУМ
Виконай завдання
Завдання 1. (13,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю
Завдання 2.(20,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю
Завдання 3. (27,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю http://zagadki.org.ua/ua/riddles/logical/
Завдання 3. (27,05) Розбери задачі за посиланням. Вибери 4 задачі, запиши їх у зошит і пришли вчителю http://zagadki.org.ua/ua/riddles/logical/
8, 15, 22, 29 квітня, 6 травня
Тема 7. Логічний практикум
1)Способи вирішення
логічних задач: метод графів, метод рівнянь, метод таблиць.
Метод графів (8 квітня)
1. Переглянь конспект уроку та розібрані задачі, приклади "Графи"
Завдання для самостійного опрацювання.
Розв'язати і прислати вчителю.
Термін виконання до 15 квітня.
2. Переглянь і розбери Задачі оптимізації на графах
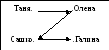
Метод таблиць (15 квітня)
1. Розглянь метод і приклади
Метод рівнянь (22 квітня)
Метод графів (8 квітня)
1. Переглянь конспект уроку та розібрані задачі, приклади "Графи"
Завдання для самостійного опрацювання.
«Змагання »
Під час змагань із стрибків у довжину Ірина, Наталка та Оксана посіли три перших місця. Яке місце посіла кожна з дівчат, якщо Наталка посіла не друге і не третє місце, а Оксана – не третє? (підказка)Розв'язати і прислати вчителю.
Термін виконання до 15 квітня.
2. Переглянь і розбери Задачі оптимізації на графах
Задачі, що розв’язуються за допомогою графів
1. Уважно прочитай задачу.
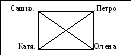
Сашко, Катя, Петро та Олена грали у теніс. Усі вони зіграли друг з другом по одному разу. Які пара гравців були?
- Про що говориться у задачі? Як звали дітей? Скільки дітей могли одночасно грати? Тобто, вони грали парами. Скільки партій зіграв кожний? Чому ти так вважаєш?
- Постав стільки крапок, скільки дітей грали у шахи та підпиши їхні імена.

- З ким з дітей міг зіграти Сашко? Поєднай крапку, що позначає Сашка з крапками, що позначають дітей, з якими він зіграв за допомогою ліній. Тепер розглянемо, з ким грав Петро. Чи є в нас вже якась лінія від його імені? З ким він грав? З ким ще грав Петро? Давай поєднаємо лініями його ім’я з цими дітьми. Розглянь крапку біля Катиного імені. З ким з дітей Катя грала, що вже позначено? Поєднай її з іншими дітьми. Хто в нас ще залишився? Скільки усього партій зіграла Олена? Яких її партнерів ми вже знаємо? З ким ще вона могла зіграти? Поєднай лінією. Уважно роздивись лінії, що поєднують імена дітей. Що цікавого ти помітив? Скільки ліній виходить з кожної крапки? Чи усі вершини вони поєднують?
- Підрахуй кількість ліній на малюнку. Скільки їх? Скільки усього ігор зігране?
У математиці схеми, схожі на дану називають графами.
2. Самостійно склади граф-креслення та розв’яжи таку задачу:
Три друга Вася, Петро та Дмитро грали у шахи. Кожний зіграв з двома іншими хлопчиками. Скільки усього партій зіграні?
3. Прочитай задачу. Друзі грали у шахи. Усього вони зіграли 10 партій. Скільки друзів грали у шахи?
- Чи можемо ми розв’язати задачу, як попередні? Чи відомо нам, скільки крапок треба поставити, тобто скільки людей грало у шахи?
- Тоді спробуємо використати метод підбору. Почнемо, наприклад з 4 гравців. Постав 4 крапки, та визнач, скільки партій могли зіграти 4 друга. Тобто, 4 друга могли зіграти 6 партій. А скільки партій зіграні? Тоді спробуємо поставити 5 крапок. Якщо друзів було 5, скільки партій вони зіграли? Визнач це за допомогою графа. Так, вони зіграли 10 партій. Чи відповідає це умові задачі? Яка буде відповідь, скільки було гравців?
4. Розв’яжи задачу. Діти пішли у ліс по ягоди. Таня йшла позаду Олени, Сашко – позаду Галини, а Олена позаду Сашка. У якому порядку йдуть діти?
- Про що говориться у задачі? Спробуй самостійно побудувати граф, що відповідає умові задачі. Чи можна за таким графом визначити, хто йде позаду, Галя чи Таня?
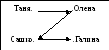
- Це неможливо. Тому спробуємо використовувати не лінії, а стрілочки. Поєднай точки за допомогою стрілочок: від того, хто йде позаду до того, хто попереду. Чи можна тепер відповісти на питання задачі?
- Хто з дітей йде останнім? А хто першим?
5. Самостійно розв’яжи задачу. Таня, Маша та Катя – подруги. Маша доросліша за Таню, а Катя молодша за Таню. Хто з дівчат молодший за всіх?
- Склади граф, познач відношення за допомогою стрілочок.
6. Уважно прочитай задачу. Катя, Тетяна та Лера пекли пироги з суницею, вишнею та яблуками. Хто який пиріг пік, якщо Лера пекла пиріг не з вишнею та не з яблуками, а Катя – не з вишнею.
- ПК СТ Вро що говориться у задачі? Як звали дівчат? Які пироги вони пекли? Скільки було дівчат?Л Я
- Постав на папері з одного боку стільки крапок, скільки дівчат, а з іншого стільки крапок, скільки було пирогів та познач буквами. В нас є два види дії, що робили дівчата з пирогами:
п екла
екла
 екла
екла
н е пекла
е пекла
 е пекла
е пекла- Позначимо їх відрізками різного кольору, наприклад червоного та синього.
- Що нам відомо про Леру? Єднай червоними відрізками Леру з тими пирогами, що вона не пекла. Що відомо ще? Поєднай Катю з пирогом, що вона не пекла. Відрізком якого кольору ти це зробиш? Чому?
- Ми отримали такий граф:
- П
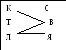
 одивись уважно на нього. Чи можна визначити, який пиріг пекла Лера? Познач це на графі. Якою лінією ти це позначиш? Чому?
одивись уважно на нього. Чи можна визначити, який пиріг пекла Лера? Познач це на графі. Якою лінією ти це позначиш? Чому? - А які пироги могла пекти Катя? Але пиріг із суницею пекла Лера, тобто який пиріг пекла Катя? Познач це.
- Який пиріг пекла Таня? Чому ти так вирішив?
7. Спробуй розв’язати таку задачу: Три товариша Сашко, Петро та Дмитро мають прізвища Олександрів, Петрів та Дмитрів. Відомо, що фамілія Сашка не Олександрів та не Дмитрів. Фамілія Дмитра не Дмитрів. Які фамілії кожного хлопчика?
Метод таблиць (15 квітня)
1. Розглянь метод і приклади
Розв'язування логічних задач табличним способом
Практична робота
- Створи в своїй папці документ Word, назови его «Логічна задача. метод таблиць»
- Побудуй таблицу за зразком
- Розвяжи логічну задачу
- Збережи роботу. Розв'язати і прислати вчителю.Термін виконання до 15 квітня.
Метод рівнянь (22 квітня)
Опрацюй матеріал Метод рівнянь
Розвяжи за допомогою рівнянь і пришли вчителю
- За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг меньше, чем в первый, а в третий – в 3 раза больше, чем во второй. Сколько килограммов апельсинов было продано в первый день
2) Розв’язування логічних задач. (29 квітня, 6 травня)
ДОТЕПНІ ЗАДАЧІ З ЛОГІКИ
Завдання. Вибери 4 задачі, можна з інтернета, можна зі збірників.
Роботу можна виконати в текстовому редакторі, або в зошиті - вибери задачі, запиши їх умови, спосіб розв'язання який вибрав, і саме розв'язання. до 13 травня
Збірник 1
10, 18, 25 березня
Тема 6. Логічні основи теорії аргументації
1) Поняття доказу і його структури. Види аргументів. Пряме і непряме підтвердження. (10 березня)
2) Поняття спростування та його види. Правила доказового міркування. Логічні помилки в доказах.(18 березня)
3) Поняття софізму і логічних парадоксів. Мистецтво ведення дискусії. (25 березня)
1. Опрацюй презентацію1, Логічні основи аргументації
2. Опрацюй теоретичний матеріал
3. Виконай завдання
Завдання 2.
Завдання 3.
Завдання 4.
Додаткова література
1. Розділ. Аргументація.
http://philosophy.univ.kiev.ua/uploads/editor/Files/LIBRARY/KONVERSKII/11.pdf
Література:
1) Арутюнов В. Х., Кирик Д. П., Мішин В. М.. Логіка: Навч. посібник для економістів. — Вид. 2-ге, допов. і перероб. — К.: КНЕУ,2000. — 144 с.. 2000
https://scicenter.online/logika-uchebnik-scicenter/logika-navch-posibnik-dlya-ekonomistiv-vid.html
https://scicenter.online/logika-scicenter/plani-seminarskih-zanyat-170123.html
https://scicenter.online/logika-scicenter/rozvyazannya-zadach-prostiy-kategorichniy-170124.html
2)Діденко Н.Г., Огородник В.Й. Навчально-методичний посібник з дисципліни “Логіка” (для студентів ОКР "бакалавр" напряму підготовки "Право"). – Донецьк: ДонДУУ, 2010. – с.
https://studfile.net/preview/5349412/
https://studfile.net/preview/5349412/page:48/
3) Електронні книги
https://stud.com.ua/logika/
4) Електронні книги
https://pidruchniki.com/logika/
5) Тести з предмету "Логіка"
https://studopedia.su/13_54437_peredmova.html
Завдання 3.
Завдання 4.
Додаткова література
1. Розділ. Аргументація.
http://philosophy.univ.kiev.ua/uploads/editor/Files/LIBRARY/KONVERSKII/11.pdf
Література:
1) Арутюнов В. Х., Кирик Д. П., Мішин В. М.. Логіка: Навч. посібник для економістів. — Вид. 2-ге, допов. і перероб. — К.: КНЕУ,2000. — 144 с.. 2000
https://scicenter.online/logika-uchebnik-scicenter/logika-navch-posibnik-dlya-ekonomistiv-vid.html
https://scicenter.online/logika-scicenter/plani-seminarskih-zanyat-170123.html
https://scicenter.online/logika-scicenter/rozvyazannya-zadach-prostiy-kategorichniy-170124.html
2)Діденко Н.Г., Огородник В.Й. Навчально-методичний посібник з дисципліни “Логіка” (для студентів ОКР "бакалавр" напряму підготовки "Право"). – Донецьк: ДонДУУ, 2010. – с.
https://studfile.net/preview/5349412/
https://studfile.net/preview/5349412/page:48/
3) Електронні книги
https://stud.com.ua/logika/
4) Електронні книги
https://pidruchniki.com/logika/
5) Тести з предмету "Логіка"
https://studopedia.su/13_54437_peredmova.html








Немає коментарів:
Дописати коментар